¿Alguna vez te has topado con un número decimal y te has preguntado cómo transformarlo en una fracción? Pues, es que, muchos de nosotros hemos estado justo ahí. Es una habilidad muy útil, sobre todo cuando estás trabajando con recetas de cocina, proyectos de carpintería, o simplemente tratando de darle sentido a los números en tu día a día. Saber cómo hacer esto, la verdad, te da una forma diferente de ver los números, y también te ayuda a entenderlos mejor.
Aprender a pasar de decimales a fracciones puede parecer un poco como magia al principio, pero, créeme, es solo cuestión de seguir unos pasos claros. Es un conocimiento básico que, de alguna manera, te abre puertas en el mundo de las matemáticas, haciendo que muchos problemas se sientan menos complicados. Así que, si te sientes un poco perdido con los números, o si buscas una manera más sencilla de manejar las cifras, este es el lugar para ti.
Aquí vamos a desglosar todo, paso a paso, para que puedas sentirte seguro al hacer estas conversiones. Vamos a ver los diferentes tipos de decimales y cómo cada uno tiene su propio truco para convertirse en una fracción. Es, en verdad, una habilidad que te servirá mucho, y, ya verás, no es tan difícil como parece. Es casi como agregar una herramienta más a tu caja de conocimientos, ¿verdad?
Tabla de Contenidos
- ¿Qué Son los Decimales y las Fracciones?
- ¿Por Qué Es Importante Saber Convertir?
- Cómo Convertir Decimales Exactos a Fracciones
- Cómo Convertir Decimales Periódicos Puros a Fracciones
- Cómo Convertir Decimales Periódicos Mixtos a Fracciones
- La Importancia de Simplificar Fracciones
- Preguntas Frecuentes sobre la Conversión
- Consejos para Practicar y Dominar
¿Qué Son los Decimales y las Fracciones?
Los decimales y las fracciones son, en el fondo, dos maneras de mostrar partes de un todo. Un decimal usa un punto para separar los números enteros de las partes más pequeñas. Por ejemplo, 0.5 significa la mitad de algo. Es una forma bastante directa de escribir números que no son completos, ¿sabes?
Las fracciones, por otro lado, usan un número arriba (el numerador) y un número abajo (el denominador), separados por una línea. El número de arriba te dice cuántas partes tienes, y el de abajo te dice en cuántas partes iguales se dividió el todo. Por ejemplo, 1/2 también significa la mitad. Ambos son, en realidad, muy útiles, solo que se ven diferentes.
Así que, a pesar de sus apariencias distintas, representan lo mismo. Entender cómo se relacionan te da una ventaja, pues te permite elegir la forma que mejor se ajuste a lo que necesitas en un momento dado. Es, de alguna manera, tener más opciones para trabajar con números.
¿Por Qué Es Importante Saber Convertir?
Saber cómo convertir decimales a fracciones es, en verdad, una habilidad que te ayuda mucho en la vida diaria. Imagina que estás cocinando y tu receta te pide 0.75 tazas de harina. Si solo tienes una taza medidora con marcas de fracción, saber que 0.75 es lo mismo que 3/4 te salva el día, ¿verdad? Es muy práctico.
Además, para cosas como las finanzas o la ciencia, a veces es más claro ver los números como fracciones. Una fracción puede mostrar la relación entre dos cantidades de una forma que un decimal no siempre hace tan evidente. Por ejemplo, 1/3 te dice que es una de tres partes, lo que es, a veces, más fácil de visualizar que 0.3333...
Y para los estudiantes, es, de hecho, una parte muy importante de las matemáticas. Te ayuda a entender conceptos más avanzados y a resolver problemas con mayor facilidad. Es como construir una base sólida para futuros aprendizajes. Es una de esas cosas que, una vez que la tienes, te das cuenta de lo útil que es.
Cómo Convertir Decimales Exactos a Fracciones
Los decimales exactos son los más sencillos de convertir, la verdad. Son aquellos que tienen un número finito de cifras después del punto decimal. Por ejemplo, 0.5, 0.25, o 1.75. No tienen números que se repiten sin fin. Son, digamos, muy directos y fáciles de manejar.
Paso a Paso para Decimales Exactos
Aquí te explico cómo hacerlo, es bastante simple:
Escribe el decimal sin el punto: Toma el número decimal y quítale el punto. Ese número será tu numerador.
Determina el denominador: Para el denominador, escribe un 1 seguido de tantos ceros como cifras haya después del punto decimal. Si hay una cifra después del punto, pones un 10. Si hay dos, un 100, y así. Es, en cierto modo, bastante lógico.
Simplifica la fracción: Una vez que tienes la fracción, simplifícala a su forma más pequeña. Esto significa dividir tanto el numerador como el denominador por el mismo número hasta que ya no puedas dividirlos más. Es muy importante hacer esto para tener la versión más limpia de la fracción.
Ejemplos de Decimales Exactos
Vamos a ver unos ejemplos para que quede bien claro:
Ejemplo 1: Convertir 0.5 a fracción
Paso 1: Escribe el número sin el punto. Es 5.
Paso 2: Hay una cifra después del punto (el 5). Así que el denominador es 10.
Paso 3: La fracción es 5/10. Ahora simplificamos. Ambos números se pueden dividir por 5. 5 ÷ 5 = 1 y 10 ÷ 5 = 2. La fracción simplificada es 1/2. Es, de hecho, bastante rápido.
Ejemplo 2: Convertir 0.25 a fracción
Paso 1: El número sin el punto es 25.
Paso 2: Hay dos cifras después del punto (el 2 y el 5). El denominador es 100.
Paso 3: La fracción es 25/100. Simplificamos. Ambos se pueden dividir por 25. 25 ÷ 25 = 1 y 100 ÷ 25 = 4. La fracción simplificada es 1/4. Es muy similar al anterior, ¿verdad?
Ejemplo 3: Convertir 1.75 a fracción
Paso 1: El número sin el punto es 175.
Paso 2: Hay dos cifras después del punto (el 7 y el 5). El denominador es 100.
Paso 3: La fracción es 175/100. Simplificamos. Ambos se pueden dividir por 25. 175 ÷ 25 = 7 y 100 ÷ 25 = 4. La fracción simplificada es 7/4. Esta es una fracción impropia, lo cual está bien.
Cómo Convertir Decimales Periódicos Puros a Fracciones
Los decimales periódicos puros son aquellos donde una o más cifras se repiten sin fin justo después del punto decimal. Un ejemplo clásico es 0.3333... (que se escribe como 0.3 con una línea encima del 3). Otro sería 0.121212... (0.12 con una línea sobre el 12). Son, en verdad, un poco más complejos que los exactos, pero tienen su truco.
Paso a Paso para Decimales Periódicos Puros
Este método es un poco diferente, así que presta atención:
Escribe el número que se repite: Toma las cifras que se repiten (el "período") y escríbelas como tu numerador.
Determina el denominador: Para el denominador, escribe tantos nueves como cifras tenga el período. Si el período tiene una cifra, pones un 9. Si tiene dos, pones dos 9s (99), y así. Es, de alguna manera, una regla especial para estos casos.
Simplifica la fracción: Al igual que antes, simplifica la fracción a su expresión más simple. Siempre busca el máximo común divisor para hacerla lo más pequeña posible. Esto es, en realidad, muy importante para el resultado final.
Ejemplos de Decimales Periódicos Puros
Veamos cómo funciona con algunos ejemplos:
Ejemplo 1: Convertir 0.333... a fracción
Paso 1: El número que se repite es 3. Ese es nuestro numerador.
Paso 2: Solo hay una cifra que se repite (el 3). Así que el denominador es 9.
Paso 3: La fracción es 3/9. Simplificamos dividiendo ambos por 3. 3 ÷ 3 = 1 y 9 ÷ 3 = 3. La fracción simplificada es 1/3. Es un clásico, ¿verdad?
Ejemplo 2: Convertir 0.121212... a fracción
Paso 1: El número que se repite es 12. Ese es nuestro numerador.
Paso 2: Hay dos cifras que se repiten (el 1 y el 2). El denominador es 99.
Paso 3: La fracción es 12/99. Simplificamos. Ambos se pueden dividir por 3. 12 ÷ 3 = 4 y 99 ÷ 3 = 33. La fracción simplificada es 4/33. Es, en cierto modo, un poco más complejo, pero sigue la misma lógica.
Ejemplo 3: Convertir 0.777... a fracción
Paso 1: El número que se repite es 7. Ese es nuestro numerador.
Paso 2: Solo hay una cifra que se repite (el 7). El denominador es 9.
Paso 3: La fracción es 7/9. Esta fracción no se puede simplificar más, ya que 7 es un número primo y 9 no es múltiplo de 7. Así que, 7/9 es la respuesta final. Es muy directo, ¿verdad?
Cómo Convertir Decimales Periódicos Mixtos a Fracciones
Los decimales periódicos mixtos son un poco más elaborados. Tienen una parte decimal que no se repite (el "anteperíodo") seguida de una parte que sí se repite (el "período"). Un ejemplo sería 0.1666... (donde el 1 no se repite y el 6 sí). Otro es 0.2343434... (donde el 2 no se repite y el 34 sí). Son, digamos, una combinación de los dos tipos anteriores.
Paso a Paso para Decimales Periódicos Mixtos
Este proceso es el más detallado de los tres, así que vamos con calma:
Forma el numerador: Toma el número completo sin el punto decimal (incluyendo la parte no periódica y la periódica). A este número, réstale la parte no periódica (el número antes del período). Ese será tu numerador. Es, en verdad, el paso más importante aquí.
Forma el denominador: Para el denominador, escribe tantos nueves como cifras tenga el período, seguidos de tantos ceros como cifras tenga el anteperíodo (la parte no periódica después del punto). Por ejemplo, si el período tiene 2 cifras y el anteperíodo tiene 1, el denominador será 990. Es, de alguna manera, una combinación de las reglas anteriores.
Simplifica la fracción: Como siempre, simplifica la fracción resultante a su mínima expresión. Divide el numerador y el denominador por su máximo común divisor. Esto te dará el resultado más claro. Es muy importante no olvidar este paso.
Ejemplos de Decimales Periódicos Mixtos
Vamos a ver cómo se hace con algunos ejemplos:
Ejemplo 1: Convertir 0.1666... a fracción
Paso 1: Numerador: El número completo sin el punto es 16. La parte no periódica es 1. Así que, 16 - 1 = 15. Este es nuestro numerador.
Paso 2: Denominador: El período tiene una cifra (el 6), así que un 9. El anteperíodo tiene una cifra (el 1), así que un 0. El denominador es 90.
Paso 3: Simplificar: La fracción es 15/90. Ambos se pueden dividir por 15. 15 ÷ 15 = 1 y 90 ÷ 15 = 6. La fracción simplificada es 1/6. Es, en verdad, un buen ejemplo para entenderlo.
Ejemplo 2: Convertir 0.2343434... a fracción
Paso 1: Numerador: El número completo sin el punto es 234. La parte no periódica es 2. Así que, 234 - 2 = 232. Este es nuestro numerador.
Paso 2: Denominador: El período tiene dos cifras (el 34), así que dos 9s (99). El anteperíodo tiene una cifra (el 2), así que un 0. El denominador es 990.
Paso 3: Simplificar: La fracción es 232/990. Ambos son números pares, así que podemos empezar dividiendo por 2. 232 ÷ 2 = 116 y 990 ÷ 2 = 495. La fracción simplificada es 116/495. Es, de hecho, un poco más trabajo, pero se logra.
Recuerda que estas conversiones son muy útiles, y, de alguna manera, te ayudan a ver los números de forma más flexible. Puedes pensar en estos métodos como herramientas que agregas a tu "hub como" de conocimientos matemáticos, listas para usar cuando las necesites.
La Importancia de Simplificar Fracciones
Simplificar una fracción es, en realidad, un paso fundamental después de la conversión. Imagina que tienes 50/100. Aunque es correcto, es mucho más fácil de entender y trabajar con 1/2, ¿verdad? Es como limpiar tu espacio de trabajo para que todo sea más claro. Una fracción simplificada es la versión más sencilla y elegante de esa fracción.
Para simplificar, buscas el número más grande que pueda dividir tanto al numerador (el número de arriba) como al denominador (el número de abajo) sin dejar residuo. A este número lo llamamos el Máximo Común Divisor (MCD). Si no encuentras el MCD de inmediato, puedes ir dividiendo por números primos pequeños (2, 3, 5, 7, etc.) hasta que ya no puedas más. Es, de hecho, un proceso que requiere un poco de práctica.
Una fracción simplificada es más fácil de comparar con otras fracciones, de sumar, de restar, y de visualizar. Es, de alguna manera, la forma estándar en la que se espera que presentes tus resultados en matemáticas. Así que, siempre, siempre, tómate un momento para simplificar. Tu yo futuro te lo agradecerá, y tus cálculos serán mucho más manejables.
Preguntas Frecuentes sobre la Conversión
Aquí te respondemos algunas preguntas que la gente suele tener sobre este tema:
¿Cómo sé si un decimal es exacto o periódico?
Un decimal exacto termina. Por ejemplo, 0.5 o 0.75. Un decimal periódico tiene cifras que se repiten sin fin. Si ves puntos suspensivos (...) o una línea sobre uno o más números, es periódico. Por ejemplo, 0.333... o 0.1212... Es, de hecho, una distinción visual bastante clara.
¿Qué pasa si el decimal tiene un número entero antes del punto?
Si tienes un número como 2.5, puedes convertir la parte decimal (0.5) a una fracción (1/2) y luego sumarla al número entero. Así, 2.5 sería 2 y 1/2. O, puedes tratar el número completo (25 en este caso) como el numerador y seguir los pasos para decimales exactos, lo que te daría 25/10, que se simplifica a 5/2. Ambas formas son correctas y, en verdad, te llevan al mismo lugar.
¿Hay alguna calculadora en línea que haga esto?
Sí, claro que sí. Hay muchas calculadoras en línea que pueden convertir decimales a fracciones al instante. Son muy útiles para verificar tus respuestas o para cuando necesitas una conversión rápida. Sin embargo, es muy importante que entiendas el proceso por ti mismo, ya que eso es lo que te da el verdadero conocimiento. Las calculadoras son herramientas, no sustitutos del aprendizaje.
Consejos para Practicar y Dominar
La práctica es, en verdad, la clave para dominar cualquier habilidad matemática, y convertir decimales a fracciones no es la excepción. Cuanto más practiques, más fácil y rápido se volverá. No te desanimes si al principio te parece un poco lento, eso es normal. Es, de hecho, un proceso que mejora con la repetición.
Un buen consejo es empezar con decimales exactos, ya que son los más sencillos. Una vez que te sientas cómodo con ellos, pasa a los periódicos puros, y luego a los mixtos. Trabaja con diferentes tipos de números y siempre verifica tus respuestas. Puedes usar una calculadora, pero asegúrate de entender por qué la respuesta es esa. Es muy importante entender el "por qué".
También, intenta explicarle el proceso a alguien más, o a ti mismo en voz alta. Esto, a veces, ayuda a solidificar lo que has aprendido y a identificar cualquier punto donde todavía
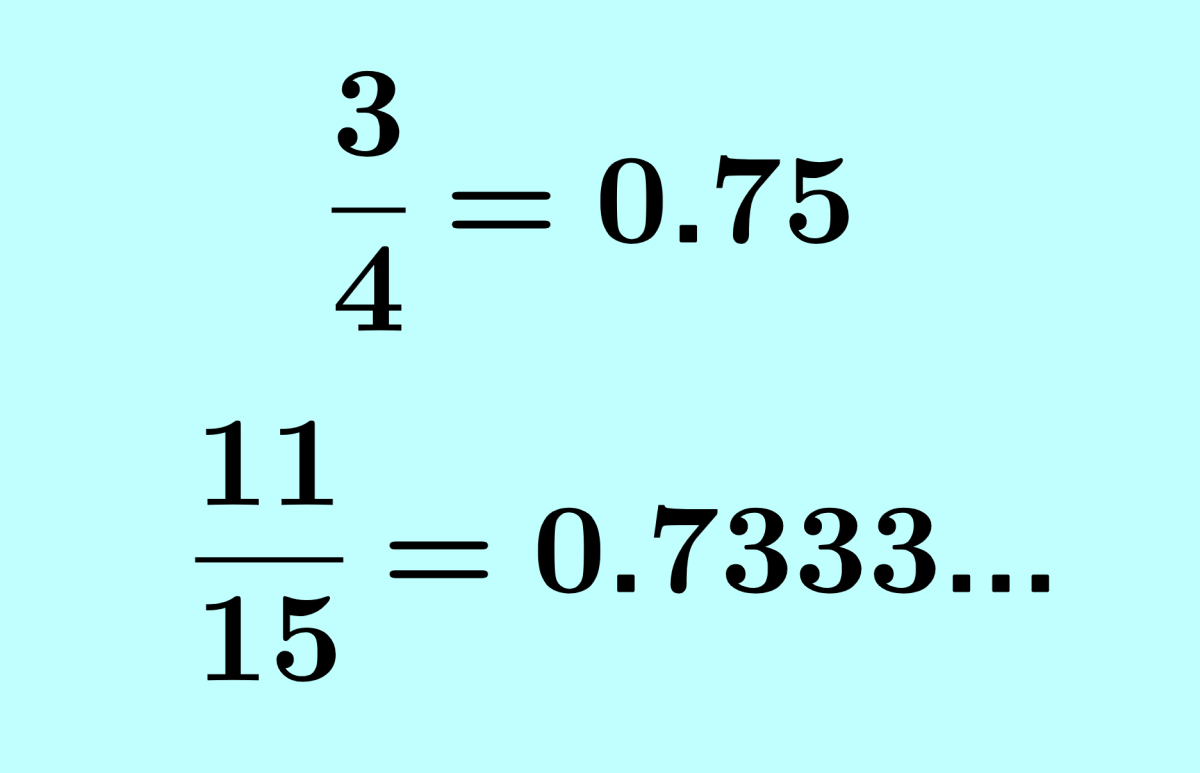


Detail Author:
- Name : Eula Brekke
- Username : emmanuelle36
- Email : ikiehn@schaden.com
- Birthdate : 2002-10-31
- Address : 387 Coy Branch Apt. 211 Boscobury, MA 66827-3970
- Phone : 405.985.4597
- Company : Kling, Stehr and Windler
- Job : Stationary Engineer
- Bio : Consectetur molestiae suscipit iste magnam. Animi quia voluptates ut quia. Vero assumenda et quia.
Socials
linkedin:
- url : https://linkedin.com/in/bednarn
- username : bednarn
- bio : Voluptatum unde illo officiis tenetur.
- followers : 4076
- following : 1772
tiktok:
- url : https://tiktok.com/@bednarn
- username : bednarn
- bio : Cupiditate culpa accusamus commodi nihil sed sunt voluptas quia.
- followers : 5030
- following : 1510

